Predicate logic

Observation 5..1  

``The completeness theorem is an absolute highlight of all of mathematics. It's brilliant'' - Dr Leader

Definition 5..2 (Arity)  

The number of arguments to a function is its arity.

Definition 5..3 (Group)   A group is a set $A$ with functions $m: A^2 \mapsto A, i: A \mapsto A, e: A^0 \mapsto A$.

$$[Associativity] (\forall x,y,z)(m(x,m(y,z)) = m(m(x,y),z)$$ (5.1)

$$[Identity] (\forall x)(m(x,e) = x \wedge m(e,x) = x)$$ (5.2)

$$[Inverse] (\forall x)(m(x,i(x)) = e \wedge e = m(i(x),x))$$ (5.3)

Definition 5..4 (Poset)  

A poset is a set A with a relation $\le \subseteq A^2$. Conveniently $\le (x,y)$ is written $x \le y$.

$$[Reflexivity] (\forall x)(x \le x)$$ (5.4)

$$[Anti-symmetry] (\forall x,y)((x \le y \wedge y \le x) \Rightarrow (x = y))$$ (5.5)

$$[Transitivity] (\forall x,y,z)((x \le y \wedge y \le z) \Rightarrow (x \le z))$$ (5.6)

Definition 5..5 (Language $L$, functions $\Omega$, predicate $\Pi$, arity function $\alpha$)  

Let the set of functions $\Omega$ and predicates $\Pi$ be distinct sets, and let the arity function be $\alpha: \Omega \cup \Pi \mapsto \mathbb{N}$. Then the language $L = L(\Omega,\Pi,\alpha)$ is the set of all formulae.

Example 5..6  

For groups, $\Omega = \{ m, i, e \}, \Pi = \emptyset$. For posets, $\Omega = \emptyset, \Pi = \{ \le \}$.

Definition 5..7 (Term)  

A term is a subset of strings of symbols from the alphabet $\Omega \cup \Pi$.

1. Every variable is a term $(x_0,x_1,\cdots)$.

2. If $f \in \Omega$, $\alpha(f) = n$ and $t_1,\cdots,t_n$ are terms then $f(t_1,\cdots,t_n)$ is a term.

Observation 5..8  

Note that the term $f(t_1,\cdots,t_n)$ is not the value of the function $f$ with these arguments. It is just a string. To emphasize this you can write it $f t_1,\cdots,t_n$.

Definition 5..9 (Atomic formula)  

An atomic formula is one of

1. $\bot$.

2. $(s = t)$ if $s,t$ are terms.

3. $\phi(t_1,\cdots,t_n)$ if $\phi \in \Pi$ and $\alpha(\phi) = n$ and $t_1,\cdots,t_n$ are terms.

Definition 5..10 (Formula)  

1. Atomic formulae are formulae.

2. If $p$ and $q$ are formulae then so is $(p \Rightarrow q)$.

3. If $p$ a formula and $x$ a variable then $(\forall x) p$ is a formula.

Definition 5..11 (Shorthands)  

$\neg p$	$(p \Rightarrow \bot )$	``not $p$''
$p \vee q$	$((\neg p) \Rightarrow q)$	``p or q''
$p \wedge q$	$\neg (p \Rightarrow (\neg q))$	``p and q''
$(\exists x) p$	$\neg (\forall x) (\neg p)$	``exists x such that p''

Definition 5..12 (Free and bound variables)  

An occurrence of a variable $x$ in a formula is free if it is not within the brackets of a ``$\forall x$''. Otherwise it is bound.

Definition 5..13 (Sentence)  

A sentence is a formula with no free variable (for example the axioms for groups and posets).

Definition 5..14 ($L$-structure)  

Let $L = L(\Omega,\Pi,\alpha)$ be a language. An $L$-structure is a non-empty set $A$, for each $f \in \Omega$ a function $f_A: A^{\alpha(f)} \mapsto A$ and for each $\phi \in \Pi$ a subset $\phi_A \subseteq A^{\alpha(\phi)}$.

Example 5..15  

$L$ the language of groups: an $L$-structure is a set $A$ with functions $m_A: A^2 \mapsto A, i_A: A \mapsto A, e_A \in A$.

$L$ the language of posets: an $L$-structure is a non-empty set with a relation $\le_A \subseteq A^2$.

Definition 5..16 (Closed term)  

A closed term is a term with no variables. For example $m(e,i(e))$, not $m(x,i(x))$.

Definition 5..17 (Interpretation of a closed term)  

The interpretation of a closed term in an $L$-structure $A$ written $t_A \in A$ is defined inductively. If $f \in \Omega$, $\alpha(f) = n$ and $t_1,\cdots,t_n$ closed terms then $f(t_1,\cdots,t_n)_A = f_A(t_{1_A},\cdots,t_{n_A})$.

Note that if $c$ is constant symbol then $c_A$ is already defined.

Definition 5..18 (Interpretation of a sentence)  

For a sentence $p \in L$ and an $L$-structure $A$ the interpretation of $p$ in $A$ is a $p_A \in \{ 0,1 \}$ defined inductively

1. $\bot _A = 0$

2. For closed terms $s,t$ $(s=t)_A = \begin{cases}1&\mbox{ if }s_A = t_A\\ 0&\mbox{otherwise}\end{cases}$.

3. For $\phi \in \Pi$, $\alpha(\phi) = n$ and closed terms $t_1,\cdots,t_n$ set
   $$\phi(t_1,\cdots,t_n) = \begin{cases}1&\mbox{if} (t_{1_A},\cdots,t_{n_A}) \in \phi_A\\ 0&\mbox{otherwise}\end{cases}$$

4. For sentences $p,q$ set $(p \Rightarrow q)_A = \begin{cases}0&\mbox{if } p_A = 1, q_A = 0\\ 1&\mbox{otherwise}\end{cases}$.

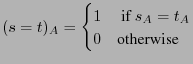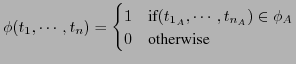
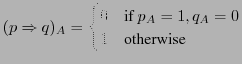5. $((\forall x)p)_A = \begin{cases}1&\mbox{if for all } a \in A \mbox{ have } p[\bar{a} / x]_A = 1\\ 0&\mbox{otherwise}\end{cases}$

   where we extend $L$ to $L'$ by adding a new constant symbol $\bar{a}$ and make $A$ an $L'$-structure by setting $\bar{a}_A = a$ and for any term $t$, $p[t/x]$ is the formula obtained by replacing each free occurrence of $x$ with $t$.

Observation 5..19  

``Now forget all this nonsense and think of it only as in the original idea.'' - Dr Leader.

Definition 5..20 (Truth, models, holds)  

If $p_A = 1$ we say $p$ holds in $A$ or $p$ is true in $A$ or $A$ is a model of $p$ written $A \models p$.

Definition 5..21 (Theory, tautology)  

For a set $T$ of sentences (a theory) say $A$ is a model of $T$ written $A \models T$ if $A \models p$ $\forall p \in T$.

For $T$ a theory, $p$ a sentence, say $T$ entails $p$ written $T \models p$ if every model of $T$ is a model of $p$.

If $\emptyset \models p$ we say $p$ is a tautology.

Observation 5..22  

What is called in propositional logic a valuation is like in predicate logic an interpretation.

Definition 5..23 (Axiomatize, axioms)  

Say that the members of a theory $T$ are axioms, and that the theory axiomatizes the things which are models of it.

Example 5..24 (Theory of groups)  

Let $L$ be the language of groups and let

$T = \{ (\forall x,y,z)(m(x,m(y,z)) = m(m(x,y),z), \\ (\forall x)(m(x,e) = x \wedge m(e,x) = x), \\ (\forall x)(m(x,i(x)) = e \wedge e = m(i(x),x)) \}$

Then an $L$-structure $A$ is a model of $T$ iff $A$ is a group. $T$ axiomatizes the class of groups.

Suppose we change the third axiom to be just $(\forall x)(m(x,i(x)) = e)$ to produce $T'$. Does $T'$ axiomatize the class of groups? (Think about it but the answer is yes).

Example 5..25 (Theory of posets)  

Let $L =$ language of posets and let $T = \{ (\forall x,y)((x \le y \wedge y \le x) \Rightarrow (x = y)), (\forall x)(x \le x), (\forall x,y,z)(((x \le y) \wedge (y \le z)) \Rightarrow (x \le x)) \}$. Then a model for $T$ is precisely a poset.

Example 5..26 (Theory of fields)  

Let $\Omega = \{ +, \times, -, 0, 1 \}$. $\Pi = \emptyset$. For $T$ take

1. Abelian group under $+,-,0$
2. Associative
3. Commutative
4. Distributive over $+$
5. $\neg (0 = 1)$
6. $(\forall x)((\neg (x = 0)) \Rightarrow ((\exists y)(x \times y = y \times x = 1))$

Then $T$ axiomatizes the class of fields.

Example 5..27 (Theory of graphs)  

Language of $\Omega = \emptyset$ and $\Pi = \{ \sim \}$. $T = \{ (\forall x) (\neg (x \sim x)), (\forall x,y)((x \sim y)\Rightarrow (y \sim x)) \}$.

Then an $L$-structure on $G$ is a $T$-model iff $G$ is a graph.

Observation 5..28  

This is called first-order logic. We can qualify over elements but not over subsets. For example we cannot say ``for all subgroups of $A$''.

Observation 5..29  

Could have an alternative language for groups with $\Omega= \{m,e \}$ and third element of the theory being $(\forall x)(\exists y)(m(x,y) = e \wedge m(y,x) = e)$.

Observation 5..30  

Many natural theories have $T$ infinite. For example, we have fields of characteristic zero. $L$ language of fields. $T =$ axioms of a field, with $\neg (1 + 1 = 0)$, $\neg (1 + 1 + 1 = 0)$ etc.

Observation 5..31  

Fields of non-zero characteristic. $L$ language of fields, $T$ axioms for a field. Can we axiomatize fields of charactistic $\ne 0$? (Exercise.)