Propositional logic

Definition 2..1 (Primitive propositions)  

$P = \{ p_1, p_2, p_3, \cdots \}$ is the set of primitive propositions.

Definition 2..2 (Proposition)  

A proposition is a subset of strings of symbols from the alphabet $(,),\Rightarrow ,\bot ,p_1,p_2,\cdots$.

Definition 2..3 (Language)  

The language $L$ (or $L(P)$) is the set of propositions

1. $P \subset L$
2. $\bot \in L$
3. if $p,q \in L$, $(p \Rightarrow q) \in L$

$L_n$ is the set of propositions of length $\le n$.

Definition 2..4 (Shorthands)  

$\neg p$	$(p \Rightarrow \bot )$	``not $p$''
$p \vee q$	$((\neg p) \Rightarrow q)$	``p or q''
$p \wedge q$	$\neg (p \Rightarrow (\neg q))$	``p and q''

Definition 2..5 (Valuation)  

A valuation is a function. $v: L \mapsto \{ 0, 1 \}$.

1. $v(\bot )=0$
2. $v(p \Rightarrow q) = \begin{cases}0&\text{if $v(p)=1,v(q)=0$}\\ 1&\text{otherwise} \end{cases}$

Theorem 2..6 (Valuations agreeing on the basic propositions are the same)  

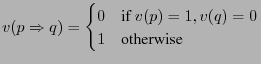
If valuations $v,v'$ have $v(p) = v'(p)$ for all $p \in P$ then $v \cong v'$.

Proof. $v = v'$ on $L_1$. If $v(p) = v'(p)$ and $v(q) = v'(q)$ then $v(p \Rightarrow q) = v'(p \Rightarrow q)$ so by induction $\forall L_n$.

$\qedsymbol$

Theorem 2..7 (A function defined on the primitive propositions can be extended to a valuation)  

Given $w: P \mapsto \{0,1\}$ there exists a valuation $v$ such that $v(p) = w(p)$ for all $p \in P$.

Proof. Let $v(p) = w(p)$ for all $p \in P$ and let $v(\bot )=0$. Extend.

$\qedsymbol$

Definition 2..8 (Model)  

If $v(p)=1$, $p$ is true in $v$. $v$ is a model of $p$.

Definition 2..9 (Tautology)   If $v(p)=1$ for all valuations $v$ then $p$ is a tautology. $\models p$.

Observation 2..10 (Techniques for proving something is a tautology)  

Draw a truth table, also note that if $v(p \Rightarrow q) = 0$ then $p = 1$ and $q = 0$.

Definition 2..11 (Semantic implication, entails)  

If $S \subseteq L$, $t \in L$ and $v(s)=1$ for all $s \in S$ means $v(t) = 1$ then $S$ entails or semantically implies $t$ ( $S \models t$). That is, every model of $S$ is a model of $t$.