Next: Two consequences of completeness Up: Logic Previous: Propositional logic Contents
All the axioms are tautologies.
Let
![]() be called the set of hypotheses or premises. A
proof of a conclusion
be called the set of hypotheses or premises. A
proof of a conclusion ![]() from
from ![]() is a finite set
is a finite set
![]() with
with ![]() and each
and each ![]() is either
is either
Then
![]() (
(![]() proves or syntactically implies
proves or syntactically implies ![]() ). If
). If
![]() then
then ![]() is a theorem (written
is a theorem (written ![]() ).
).
![]()
| 1 |
|
Axiom 2 |
| 2 |
|
Hypothesis |
| 3 |
|
Axiom 1 |
| 4 |
|
Modus ponens on 2, 3 |
| 5 |
|
Modus ponens on 4,1 |
| 6 |
|
Hypothesis |
| 7 |
|
Modus ponens on 6,5 |
![]()
| 1 |
|
Axiom 2 |
| 2 |
|
Axoim 1 |
| 3 |
|
Modus ponens on 2,1 |
| 4 |
|
Axiom 1 |
| 5 |
|
Modus ponens on 4,3 |
Let
![]() ,
, ![]() . Then
. Then
![]() iff
iff
![]() .
.
| Hypothesis | |
| Modus ponens |
Thus proving ![]() from
from
![]() .
.
![]()
Let
![]() be a proof of
be a proof of ![]() from
from
![]() . Show that
. Show that
![]() for every
for every ![]() .
.
If ![]() certainly
certainly
![]() as
as
![]() .
.
Otherwise if ![]() is an axiom or
is an axiom or ![]() , write
, write
| Axiom or Hypothesis | |
|
|
Axiom 1 |
|
|
Modus ponens |
So
![]() .
.
Otherwise ![]() was got from Modus Ponens, i.e. there exist
was got from Modus Ponens, i.e. there exist ![]() such
that
such
that
![]() . By induction on
. By induction on ![]() assume
assume
![]() and
and
![]() so write
so write
|
|
Axiom 2 |
|
|
Modus ponens |
|
|
Modus ponens |
![]()
To show
![]() show
show
![]() using
modus ponens twice.
using
modus ponens twice.
Let
![]() ,
, ![]() then
then
![]() implies
implies
![]() .
.
Certainly axioms (are tautologies) and elements of ![]() are true. Also
modus ponens: if
are true. Also
modus ponens: if ![]() and
and
![]() then
then ![]() . So
. So
![]() for all
for all ![]() in a proof of
in a proof of ![]() from
from ![]() .
.
![]()
![]() is inconsistent if
is inconsistent if
![]() . Otherwise it is
consistent.
. Otherwise it is
consistent.
A set
![]() is deductively closed if it contains all its
consequences. If
is deductively closed if it contains all its
consequences. If
![]() then
then ![]() .
.
Let
![]() be consistent. Then
be consistent. Then ![]() has a model.
has a model.
Claim. For any consistent
![]() and any
and any ![]() at least
one of
at least
one of
![]() and
and
![]() is consistent.
is consistent.
Proof of claim. Suppose
![]() is inconsistent. Then
is inconsistent. Then
![]() . So
. So
![]() so
so ![]() and
and
![]() prove the same things so
prove the same things so
![]() is consistent.
is consistent.
![]() is countable. Let
is countable. Let
![]() be an ordering of
be an ordering of ![]() . Let
. Let
![]() . Let
. Let ![]() be
be
![]() or
or
![]() choosing one which is consistent. Let
choosing one which is consistent. Let
![]() . Then for each
. Then for each ![]() at least one of
at least one of
![]() or
or
![]() .
. ![]() is consistent because proofs are finite. Also
is consistent because proofs are finite. Also ![]() deductively closed. If
deductively closed. If
![]() then
then ![]() does not prove
does not prove ![]() (as
(as
![]() ).
).
Define
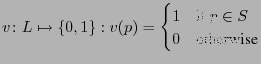 .
. ![]() is a
valuation. Proof.
is a
valuation. Proof.
![]() . If
. If
![]() then
then
![]() ,
,
![]() . So
. So
![]() so
so
![]() . If
. If ![]() then
then
![]() so
so
![]() so
so
![]() . If
. If ![]() then
then
![]() so
so
![]() . Enough to show
. Enough to show
![]() . That is,
. That is,
![]() .
.
|
|
Hypothesis |
|
|
Axiom 1 |
|
|
Axiom 3 |
So
![]() . So
. So ![]() is a valuation. So there is a model for
is a valuation. So there is a model for ![]() .
.
![]()
Previous theorem used fact that ![]() is countable (so that
is countable (so that ![]() is
countable) but this is not necessary by Zorn's lemma (next chapter).
is
countable) but this is not necessary by Zorn's lemma (next chapter).
Let
![]() ,
, ![]() . Then
. Then
![]() implies
implies
![]() .
.
![]()
Let
![]() ,
, ![]() . Then
. Then
![]() iff
iff
![]() .
.
![]()